It is trivial: To remove gases from a given volume we have to pump. We know this from pumping of liquids. However, there are fundamental differences between pumping of liquids and pumping of gases. Liquids are incompressible, at constant temperature they don’t change their volume even if highest pressures are applied. This principle is used in hydraulic power transmission.

The ”general equation of state for an ideal gas” is a good approach for the description of the behaviour of a real gas:

with

p · V = N · k · T  (1)

p = pressure
V = volume
N = total number of gas particles in V
k = Boltzmann constant (1,38 ^. 10^-23 JK^-1)
T = absolute temperature

At a constant temperature the product of pressure and volume is constant. If a given amount of gas can spread into a larger volume, pressure decreases and vice versa.

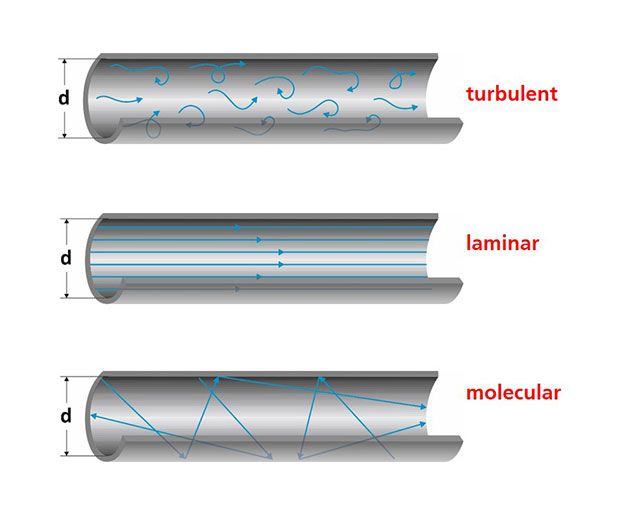
For the layout of vacuum pumping equipment, the different types of flow mechanism governing the different pressure regimes are of crucial importance (see adjacent figure).

Let us consider the flow through a pipe having a diameter d. In case of a liquid we talk about a ”viscous” flow. If there are no obstacles, the flow is ”laminar”. For such a laminar flow the speed distribution is parabolic, meaning that the highest speed can be found in the center of the pipe. ”Turbulences” are formed around obstacles.

Due to the high particle density gases at atmospheric pressure behave like liquids. The flow is viscous, if the ”mean free path” (this term was introduced in the last newsletter) is much smaller than the diameter of the pipe:

λ << d  (2)

This is the case in rough vacuum at pressures ranging from 10³ to 10⁰ mbar. In high and ultra high vacuum we are talking about ”molecular  flow”. The particle density in these regimes is very low, and collisions hardly appear, resulting in:

λ >> d  (3)

Later we will deal with various principles of pumping taking into account the different flow mechanisms.

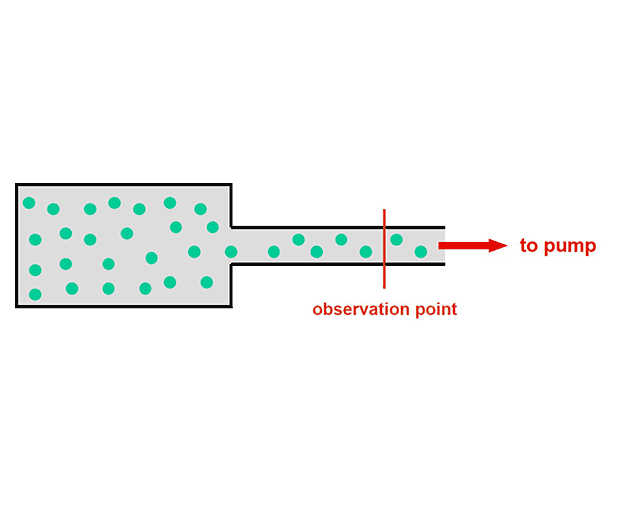
Maybe you remember: From time to time one could see persons on the roadside sitting on folding camp chairs and counting cars. I assume that meanwhile they have been replaced by modern optical devices. The picture may help us if we replace cars by gas particles passing an observation point during the evacuation of a recipient according to the adjacent figure.

Let N be the total number of gas particles (see equation (1)) in the recipient before starting the pump down process. We are interested in the particle flow

I_t = dN/dt  (4)

at our observation point. The problem is that we neither can see the particles nor can count them. So let us go back to the state equation (1) and rewrite equation (4) after introduction of a particle density n = N/V as:

I_t = n · dV/dt = (p/kT) · dV/dt   (5)

Further conversion delivers:

I = I_t kT = p · dV/dt = p · S  (6)

S = dV/dt is the volumetric flow rate through the suction hole of our vacuum pump and is named as pumping speed. The value of pumping speed maybe found on the identification plate of a vacuum pump. In the rough and fine vacuum regimes the unit is m³/h, for high and ultra high vacuum pumps l/s. The literature says that this differentiation is only historic.

The pumping speed is a measure for the ”transport capacity” of the pump and according to equation (6) gives us no information about the amount of gas transported per time unit. The latter is called throughput of the pump and given by the product p^.S according to (6). Often the term pV throughput is used.

Imagine you want to hire a truck for a relocation. A relevant number would be the loading capacity in m³. However, this information could be incomplete since you also need to know the ”mean density” of your freight in order to avoid overloading of the truck. The terms ”pumping speed” and ”pV throughput” have similar meanings. If gas pressures (and thus particle densities) are too high the pumping speed of high vacuum pumps decreases dramatically, they can work efficiently only in a certain pressure region.

Hence, the pumping speed itself is a function of pressure, and the amount of transported gas or pV throughput q_pV is:

q_pV = p · S(p)  (7)

Identification plates of high vacuum pumps often show impressive pumping speed numbers which might be irritating for a person not being a specialist in vacuum technology. Oil diffusion pumps are built with pumping speeds up to S = 50.000 l/s, and the biggest turbomolecular pumps have S = 5.000 l/s. (Imagine a water pump with a transport capacity of 50 m³ per second!) One has to take into account that these numbers are valid only for pressures below 10^-3 mbar, this pressure results in a pV throughput of 50 mbar ^. l/s for the diffusion pump and 5 mbar ^. l/s for the turbomolecular pump.

We will learn more about conductance values and various types of vacuum pumps in the next issue of this newsletter.

To the overview