What is actually a ”quantum lap”?
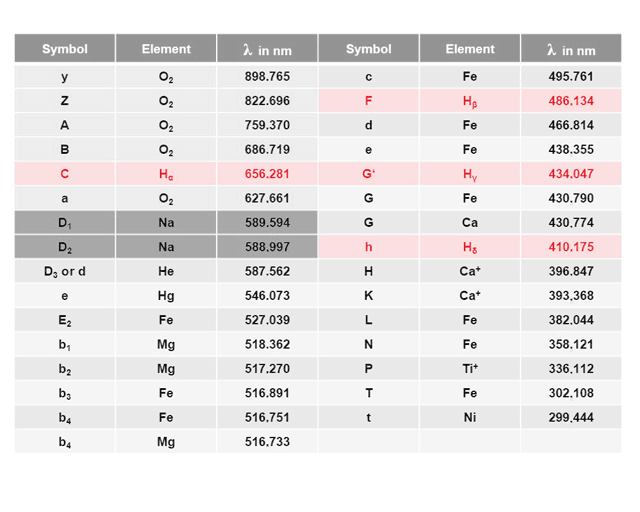
I have taken the seventieth birthday of the Fraunhofer Gesellschaft in 2019 as an opportunity to take a closer look at the quantum leap. After all, the famous Fraunhofer lines which, hopefully, everyone among us has already heard about at sometime or another, are direct consequences of quantum leaps. Around 1814 our namesake Joseph von Fraunhofer discovered around 570 mysterious black lines, some of which are listed in the Table below, in the emission spectrum of the sun. He catalogued them meticulously, but was unable to explain their origin; this would have indeed been impossible back then, without the modern physics of the 20th century. If, for example, sunlight is broken down into its spectral colors through a high-resolution optical grating, “the corresponding colors are missing at the positions of the Fraunhofer lines”.
The radiation spectrum of the sun spans a wavelength range from around 300 nm (ultraviolet) to 3000 nm (infrared). The visible part (light) lies between 400 nm and 750 nm; it is formed in one of the outer “shells”, the photosphere. If certain individual wavelengths from the above-mentioned range are absorbed by atoms present in the photosphere, black lines form at these positions in the spectrum, which provide practical information concerning the ” fingerprint” or “DNA“ of these atoms. Herein lies the significance of Fraunhofer's work, and for this reason his original tombstone, destroyed in World War II, bore the inscription
“Approximavit Sidera” – He brought us closer to the stars
The prominent Fraunhofer lines include the transitions from the Balmer series of the hydrogen atom highlighted in red in the adjacent Table and catalogued by Fraunhofer under C, F, G' and h. We therefore want to take a closer look at the possible energy levels of the hydrogen atom. In 1885, Johann Balmer established the following relationship for the transitions between discrete energy states:
λ = A (n²/(n²-4)) (1)
With the empirical constants A = 364.57 nm and n = 3, 4, 5, 6 the wavelengths of the four aforementioned Fraunhofer lines and the Balmer lines Hα, Hβ, Hγ, Hδ are obtained (see the Figure below on the left).
Johannes Rydberg generalized the Balmer formula to
1/ λ = RH (1/m2 – 1/n2) (2)
with: RH = 1,097 x 107 m-1 (Rydberg constant for hydrogen)
m = 1, 2, 3, ….
n = 2, 3, 4, …
For the special case of m = 2 and n = 3, 4, 5, 6, ... this results in the Balmer series.
Around 100 years after Fraunhofer's discovery, Niels Bohr explained the spectra of the H atom with his postulates in 1913. In doing so, he created the foundation for understanding the structure of the atoms and, thereby, also the comprehensive explanation for the formation of the Fraunhofer lines.
According to Bohr, the electron in the hydrogen atom can assume various excited states in addition to the ground state, i.e. it can be lifted to an energetically higher orbit through the irradiation of external energy in the form of a light quantum. When “falling back” into the ground state, the corresponding quantity of energy is re-emitted; depending on the wavelength, light of a specific color is thereby produced. The absorbed or emitted quantities of energy are not arbitrary, but are instead “quantized” in accordance with equation (2).
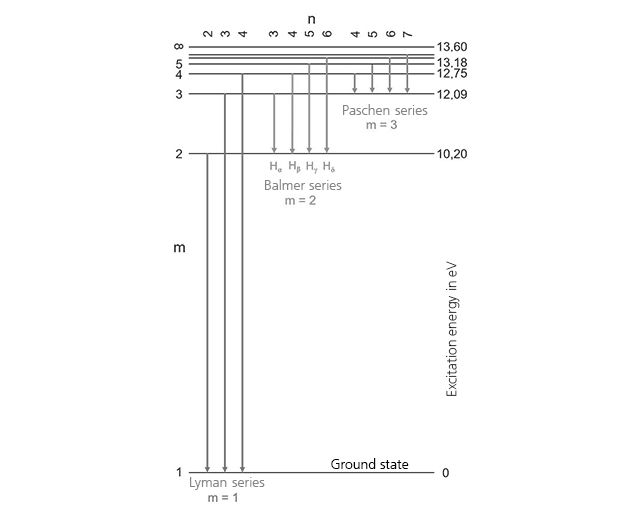
The adjacent Figure shows the Grotrian diagram for the hydrogen atom. The limit energy for ionization (i.e. the complete detachment of the electron from the atomic core) is 13.60 eV. All possible quantum leaps for hydrogen must therefore lie below this limit energy. In the periodic table of elements, helium possesses the highest ionization energy, with 24.60 eV.
As the basis for our calculation examples, we select the most energetic of the lines drawn in the adjacent Figure, the transition 4 à 1 of the Lyman series. With an energy difference of 12.75 eV, this is, from an atomic point of view, a huge quantum leap.
Dear reader, who would talk about quantum leaps in connection with the forward movement of a snail? The term “snail's pace” requires no further explanation. The snail, which moves at a typical speed of 3.6 meters per hour, is considered to be one of the slowest living creatures on earth. And yet: Its kinetic energy is equivalent to 7 billion quantum leaps.
Conversely, if we give the snail the energy of our selected quantum leap, we slow it down to 10-8 m/s. In 24 hours, it then manages about one millimeter - which is only twice as fast as the growth rate of human hair.
Even a Fraunhofer employee, driving his car at 150 km/h on the highway in happy anticipation of a customer order (and thereby violating the guidelines stipulated by his employer) is nothing unusual in our everyday life. He can only shake his head concerning the quantum leap, as he is driving with an energy content of 4 x 1023 quantum leaps!
Finally, a comparison from high-energy physics: In a single nuclear fusion reaction, in which two hydrogen isotopes fuse to form a helium atom, an energy of 17.6 MeV is released as a result of the mass defect in accordance with Einstein's equation E = mc²; this corresponds to more than one million quantum leaps of the energy difference of 12.75 eV in the hydrogen atom.
So, dear reader, please be a little cautious in the future if you want to use the quantum leap as a synonym for a particularly exciting development. It is only a tiny waft of energy package, the gentle movement of air when a butterfly beats its wings compared to a hurricane. The term “disruptive” is currently also very chic, is it not?
Last modified: