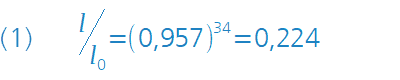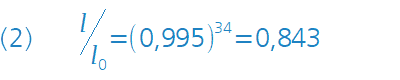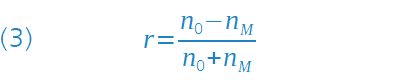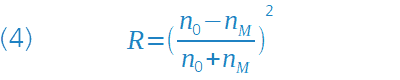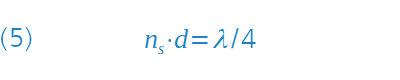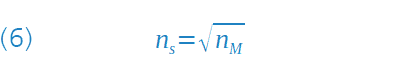Wie macht man Glas eigentlich »unsichtbar«?
Der Werkstoff Glas fasziniert durch eine Reihe von herausragenden Eigenschaften. Die wichtigste ist seine hohe Transparenz im gesamten sichtbaren Spektrum, sie ermöglicht einen farbneutralen Blick in die Außenwelt. Lassen Sie uns aber auch einen Blick auf die weniger angenehmen Eigenschaften des Glases werfen. Eine Glasscheibe reflektiert etwa 8,3 Prozent des einfallenden Lichts und wirkt somit (vor allem vor dunklem Hintergrund) wie ein schwacher Spiegel. Im täglichen Leben mögen diese Reflexe kaum stören, bei hochwertigen optischen Komponenten sind sie allerdings nicht tolerierbar.
Am Beispiel des Zoom-Objektivs (Brennweitenbereich 55 mm – 300 mm) eines renommierten Kameraherstellers soll dies demonstriert werden. Das Objektiv besteht aus 17 Einzellinsen, also 34 Glasoberflächen.
Wie in der nebenstehenden Gleichung (1) dargestellt, berechnet sich das nach dem Passieren des Objektivs auf den Bildsensor (früher: Film) fallende Restlicht zu I/I0 = (0,957)34 = 0,224. Dabei ist I0 die Lichtintensität vor Eintritt und I die verbleibende Intensität nach Austritt. Für das Reflexionsvermögen einer einzelnen Glasoberfläche wurde der Wert 0,043 [siehe Gleichung (4)] eingesetzt. Wie man dem Ergebnis entnehmen kann, liegen die Lichtverluste bei etwa 77 Prozent! Durch das Objektiv »vagabundierende« Lichtanteile, die aufgrund von Vielfachreflexionen entstehen, sorgen zudem für eine Minderung des Bildkontrastes.
Linsen mit einer hochwertigen Entspiegelung (man spricht auch von »Vergütung«) reduzieren die Restreflexion auf Werte um 0,005 (gemittelt über das sichtbare Spektrum zwischen 400 nm und 750 nm) pro Glasoberfläche. Entsprechend der Gleichung (2) I/I0 = (0,995)34 = 0,843 liegen die Lichtverluste dann nur noch bei rund 16 Prozent.
Die Wirkungsweise einer Entspiegelung oder Vergütung von optischen Oberflächen lässt sich mit dem Phänomen der Interferenz erklären. Voraussetzung dafür ist die Beschreibung des Lichts durch eine elektromagnetische Welle. Trifft eine solche Lichtwelle von einem transparenten Medium mit dem Brechungsindex n0 (im Allgemeinen ist das Luft mit n0 = 1) auf die Grenzfläche eines ebenso transparenten Mediums mit dem Brechungsindex nM, so werden die Zusammenhänge zwischen Transmission, Reflexion, Brechungsindizes und Einfallswinkel durch die Fresnel-Gleichungen beschrieben, auf deren ausführliche Diskussion hier verzichtet werden soll.
Alle Betrachtungen in diesem Artikel beziehen sich der Einfachheit halber auf senkrechten Lichteinfall. Dass Interferenzeffekte stark winkelabhängig sind, lässt sich im Alltag ständig beobachten. Schauen Sie einmal unter verschiedenen Winkeln auf Ihre entspiegelten Brillengläser oder das Objektiv eines Fernglases.
Dünne transparente Schichten auf Glas können bei geeigneten Brechungsindizes nS die resultierende reflektierte Welle auslöschen (konstruktive Interferenz) oder verstärken (destruktive Interferenz). Interferenzphänomene lassen sich nur dann beobachten, wenn die Schichtdicke im Bereich der Lichtwellenlängen liegt. Eine anschauliche Darstellung der zeitlichen und räumlichen Entwicklung von Interferenz an Grenzflächen gelingt am besten durch Animationen, die in diesem Beitrag durch einige »Momentaufnahmen« ersetzt werden sollen.
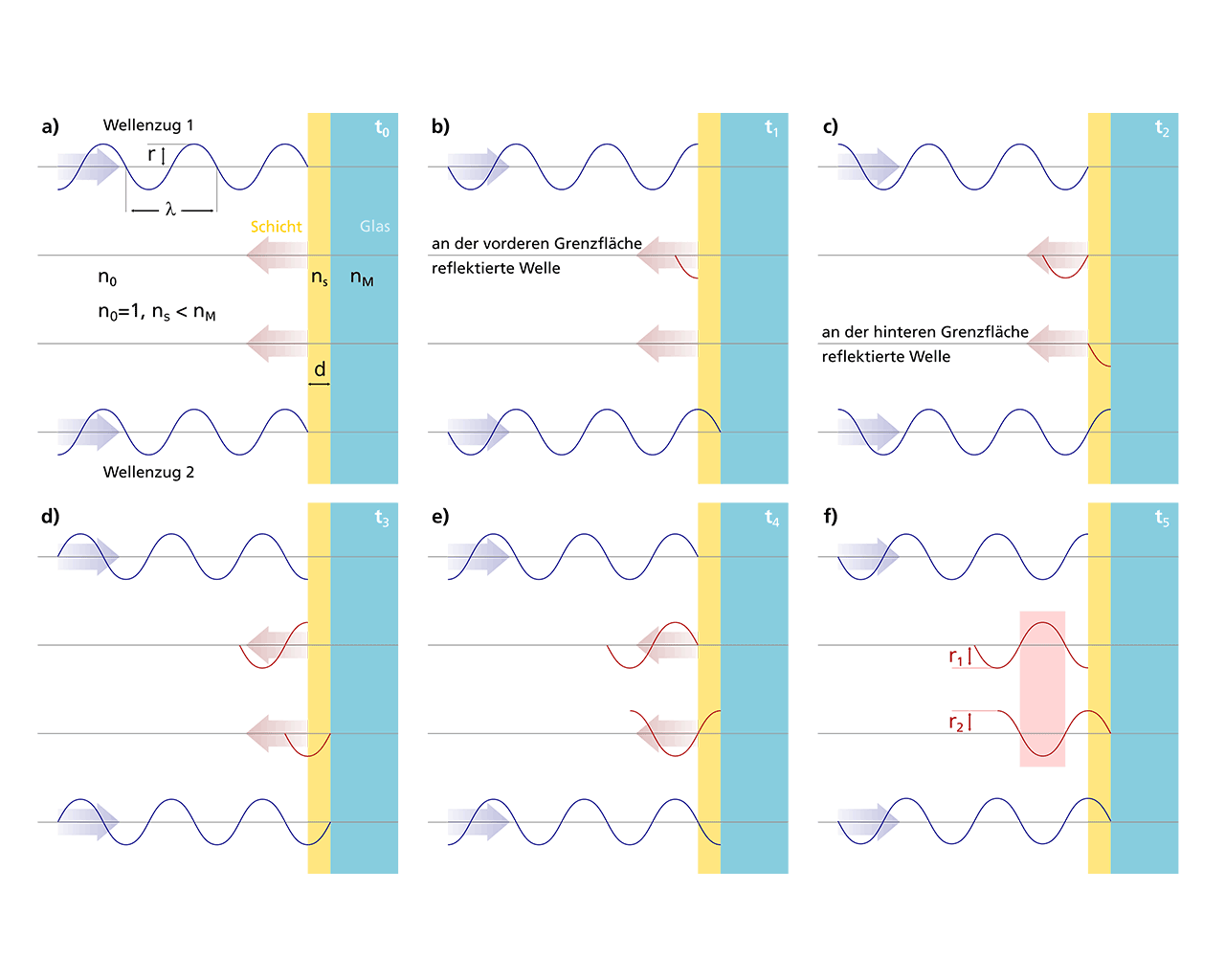
In der nebenstehenden Abbildung fallen zum Zeitpunkt t0 zwei Wellenzüge mit gleicher Amplitude r und Wellenlänge λ phasengleich auf die Grenzfläche zwischen Luft und Schicht. Die folgenden Abbildungen 1(b) bis 1(f) zeigen die Entwicklung in Zeitintervallen Δt = λ/4c0 mit der Vakuumlichtgeschwindigkeit c0 = 3 . 108 m/s.
Der an der vorderen Grenzfläche Luft – Schicht reflektierte Wellenzug eilt dem an der hinteren Grenzfläche Schicht – Glas reflektierten um die doppelte geometrische Schichtdicke voraus. Bei einem Gangunterschied von λ/2 schwingen die beiden reflektierten Teilwellen gegenphasig und löschen sich auf diese Weise aus [siehe Zeitpunkt t5 in 1(f)]. Die Schicht kann also prinzipiell das Glas (oder zumindest dessen vordere Oberfläche) »unsichtbar« machen.
Damit eine perfekte Antireflexwirkung gelingt, müssen Randbedingungen erfüllt sein. Zunächst wird aus der Darstellung ersichtlich, dass in die Schicht der Dicke d genau »eine Viertel Wellenlänge hineinpassen« muss, andernfalls ist eine Phasenverschiebung um λ/2 nicht möglich. Weiterhin ist zu beachten, dass das Licht in einem Medium mit einem Brechungsindex nS auf die Geschwindigkeit c = c0/nS »abgebremst« wird.
Die für die Ausbreitung der Welle relevante optische Schichtdicke ist also nS . d. Daraus ergibt sich als Phasenbedingung für eine Auslöschung des reflektierten Lichts: nS . d = λ/4.
Die Phasenbedingung bestimmt die Schichtdicke d, sie lässt sich natürlich nur für eine einzige Wellenlänge aus dem sichtbaren Spektrum erfüllen (»Designwellenlänge« in der Sprache der Optiker). Meistens legt man die Designwellenlänge in die Mitte des sichtbaren Spektrums (Farbe »grün« bei 550 nm). Neben der Phasenbedingung muss noch berücksichtigt werden, dass eine vollständige Auslöschung nur dann erreicht werden kann, wenn auch die Amplituden r1 und r2 der beiden reflektierten Wellenzüge gleich sind.
Wie in der nebenstehenden Formel (6) dargestellt, ergibt sich daraus unter Verwendung der Fresnel-Gleichung (3), die jetzt für beide Grenzflächen angewendet wird, nach entsprechender Umrechnung die Amplitudenbedingung für den Brechungsindex nS der Schicht.
Für die komplette Entspiegelung von Glas müsste also ein Schichtmaterial mit nS = 1,23 gefunden werden, welches die Natur leider nicht für uns bereithält. Mit jedem zur Verfügung stehenden Material wird also nur eine Teilauslöschung möglich sein. Nebenbei ist zu bemerken, dass eine Antireflexwirkung auf Glassubstraten nur durch Schichten mit nS < 1,52 zu erzielen ist, Schichten mit nS > 1,52 führen zur Reflexerhöhung. Das Phänomen kann übrigens im Alltag am »Substrat« Wasser (nM = 1,33) beobachtet werden. Dünne Benzin- oder Ölrückstände (z.B. nS = 1,50 für Benzol) auf Pfützen liefern schillernde Interferenzfarben.
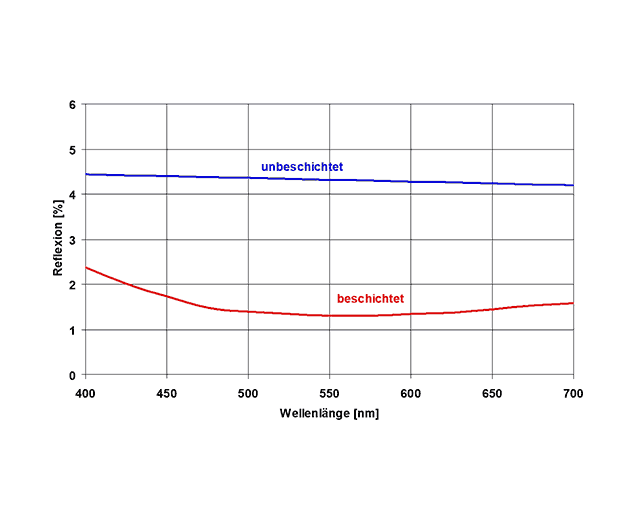
Bei der Suche nach geeigneten Schichtmaterialien mit nS < 1,52 stößt man auf MgF2 (nS = 1,38) und SiO2 (nS = 1,46). Anwendung der Fresnel-Gleichung auf MgF2 liefert R = 0,0125 für eine Glasoberfläche, die Gesamtreflexion der Scheibe verringert sich also von 8,3 Prozent auf 2,5 Prozent. Dies ist schon ein Teilerfolg, aber Potential zur Verbesserung ist noch vorhanden. Die nebenstehende Abbildung zeigt die Reflexionskurve einer λ/4 dicken MgF2-Schicht bei einer Designwellenlänge von 550 nm. Die entsprechende Schichtdicke ist nach (5) 99,6 nm.
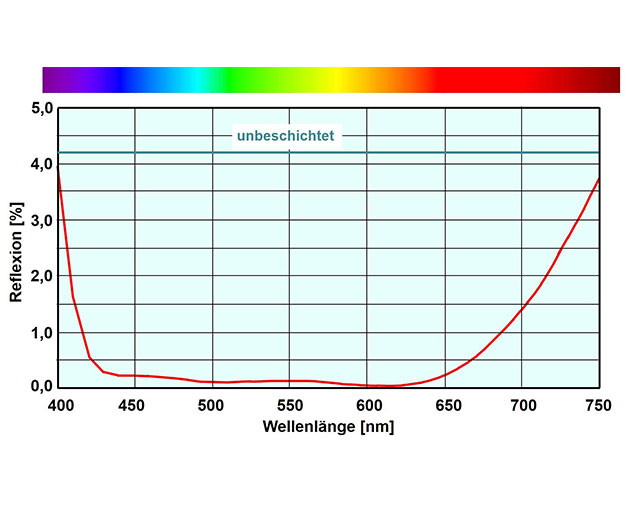
Wer bessere Entspiegelungen haben möchte, muss »Schicht um Schicht« hinzufügen, die Fresnel-Gleichungen entsprechend für mehrere Grenzflächen anwenden und sich geeignete Designs vom Computer berechnen lassen. Wir möchten uns die Beschreibung des Weges von der einfachen λ/4 MgF2-Schicht bis zur Super-Breitbandentspiegelung mit 6 oder mehr Schichten sparen. Die nebenstehende Abbildung zeigt die spektrale Reflexion für eine Breitbandentspiegelung aus vier Schichten mit Si02 (nS = 1,46) und TiO2 (nS = 2,35) als Schichtmaterial.
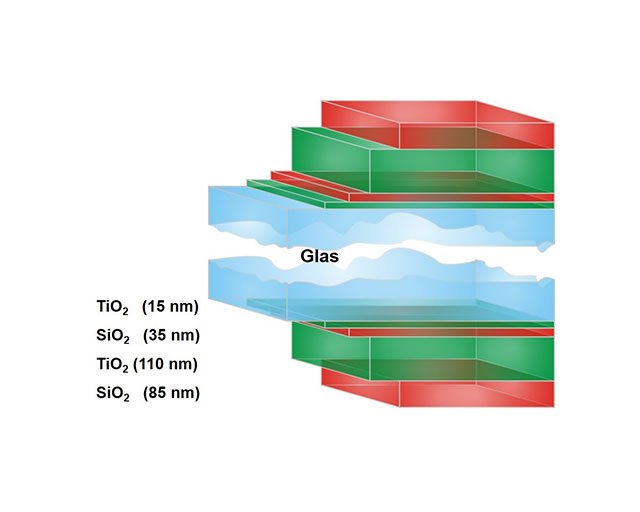
Ein Beispiel für den Schichtaufbau eines solchen Systems ist in der nebenstehenden Abbildung dargestellt. Da auch die Reflexion von der hinteren Glasoberfläche unterdrückt werden muss, ist das identische Schichtpaket auf beiden Glasoberflächen aufzubringen.
Die nebenstehende Abbildung zeigt ein Objekt hinter einer geteilten Scheibe, wobei die linke Hälfte mit einer Breitbandentspiegelung versehen ist und damit praktisch »unsichtbar« wird.
Die Reflexminderung oder -auslöschung für den sichtbaren Teil des solaren Spektrums ist nur eine der Herausforderungen, die das Glas als optischer Werkstoff oder Konstruktionselement für uns bereithält. Neben dem Licht liefert die Sonne auch Wärme im sogenannten Nahen Infrarotbereich (NIR) zwischen etwa 800 und 3000 nm. In der kalten Jahreszeit müssen zudem Räume geheizt werden, die entsprechende Temperaturstrahlung liegt mit Wellenlängen um 10 µm im Fernen Infrarot (FIR).
»Kann Glas Wärme spiegeln?« ist eine Frage, auf die wir in den kommenden Beiträgen Antworten geben werden.
Letzte Änderung: