Wie entsteht eigentlich Vakuum?
Eigentlich ist es trivial: Um Gase aus einem Behälter, also aus einem vorgegebenen Volumen zu entfernen, müssen wir pumpen, wie wir das auch von Flüssigkeiten her kennen. Allerdings gibt es wesentliche Unterschiede zwischen dem Pumpen von Flüssigkeiten und dem Pumpen von Gasen. Flüssigkeiten sind inkompressibel, d.h. ändern ihr Volumen bei konstanter Temperatur auch dann nicht, wenn höchste Drücke angewendet werden. Bekannterweise beruht die hydraulische Kraftübertragung auf dieser Inkompressibiliät.
Das Verhalten von Gasen lässt sich in guter Näherung mit der »Allgemeinen Zustandsgleichung für ideale Gase« beschreiben:
p · V = N · k · T (1)
p = Druck
V = Volumen
N = Gesamtzahl der Teilchen im Volumen V
k = Boltzmannkonstante (1,38 . 10-23 JK-1)
T = absolute Temperatur
Bei konstanter Temperatur ist das Produkt aus Druck und Volumen konstant. Wenn ich also der vorgegebenen Gasmenge mehr Raum zur Verfügung stelle, sinkt der Druck und umgekehrt.
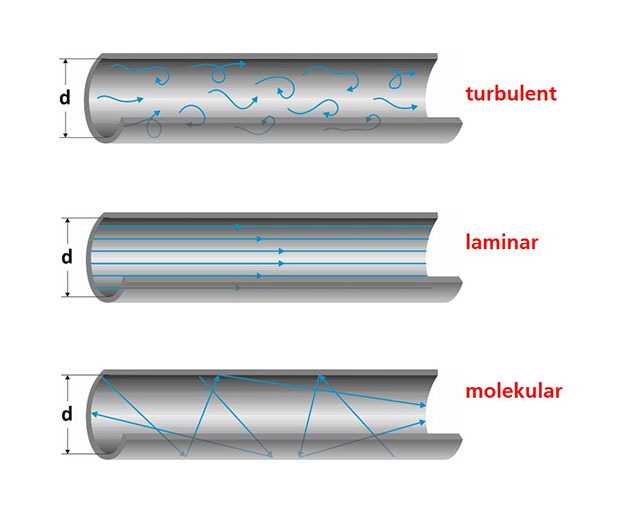
Für die Auslegung eines Vakuumpumpstandes sind die in den verschiedenen Druckbereichen vorherrschenden Strömungsarten von entscheidender Bedeutung. Sie sind in der nebenstehenden Abbildung dargestellt.
Wir betrachten die Strömung durch ein Rohr mit dem Durchmesser d. Bei der Strömung von Flüssigkeiten durch Rohre spricht man von »viskoser« Strömung. Sind keine Hindernisse im Weg, so ist die Strömung »laminar«. Laminarströmungen sind gekennzeichnet durch ein parabolisches Geschwindigkeitsprofil. Im Zentrum des Rohres erreicht die Geschwindigkeit den höchsten Wert, sie nimmt zu den Rohrwänden hin kontinuierlich ab. Um Hindernisse bilden sich »Turbulenzen«.
Gase bei Normaldruck verhalten sich aufgrund der hohen Teilchendichte annähernd wie Flüssigkeiten. Viskose Strömung tritt dann auf, wenn die »mittlere freie Weglänge« (dieser Begriff wurde im letzten Newsletter erläutert) sehr viel kleiner ist als der Rohrdurchmesser, wenn also gilt:
λ << d (2)
Dies ist im Grobvakuum, also bei Drücken zwischen 103 und 100 mbar der Fall. Im Hoch- und Ultrahochvakuum spricht man von »Molekularströmung«. Die Teilchendichte ist hier so gering, dass Stöße zwischen Teilchen kaum noch stattfinden, und es gilt:
λ >> d (3)
Mit den vielfältigen Pumpprinzipien für die verschiedenen Strömungsarten werden wir uns an späterer Stelle beschäftigen.
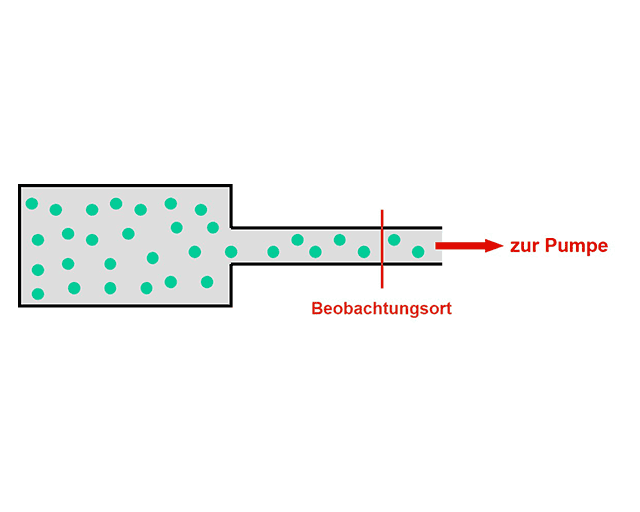
Vielleicht erinnern Sie sich: Früher hat man von Zeit zu Zeit am Straßenrand Personen auf Campingstühlen gesehen, die Fahrzeuge zählten. Heute ist diese Art der Tätigkeit wohl durch moderne Messtechnik »mit niedrigeren Löhnen« ersetzt worden. Das Bild kann hilfreich sein, wenn wir Autos durch Gasteilchen ersetzen, die entsprechend der nebenstehenden Abbildung beim Evakuieren eines Behälters einen bestimmten Beobachtungsort passieren.
Sei N die Gesamtzahl der Teilchen (siehe Gleichung (1)) in unserem Behälter (Rezipienten) vor Beginn des Pumpprozesses. Uns interessiert der Teilchenstrom
It = dN/dt (4)
am Beobachtungsort. Dieser ist allerdings nicht zugänglich, da wir die Teilchen nicht sehen und schon gar nicht zählen können. Wir behelfen uns mit der Gasgleichung (1) und schreiben Beziehung (4) nach Einführung der Teilchendichte n = N/V als:
It = n · dV/dt = (p/kT) · dV/dt (5)
Weitere Umformung ergibt:
I = It kT = p · dV/dt = p · S (6)
Die Größe S = dV/dt ist der Volumendurchfluss durch die Ansaugöffnung der Pumpe und wird als »Saugvermögen« bezeichnet. Der Hersteller der Vakuumpumpe vermerkt diese Größe in der Regel auf dem Typenschild. Für Grob- und Feinvakuumpumpen wird das Saugvermögen meist in m3/h angegeben, für Hoch- und Ultrahochvakuumpumpen in l/s. In der Literatur liest man, dass diese Unterscheidung rein historisch bedingt ist.
Das Saugvermögen gibt die »Transportkapazität« der Pumpe an und liefert entsprechend Gleichung (6) noch keine Aussage über die pro Zeiteinheit abtransportierte Gasmenge. Diese wird als »Saugleistung« bezeichnet und ist nach (6) gegeben durch das Produkt p.S. Statt des Begriffs Saugleistung verwendet man auch häufig die Alternativen Gasstromstärke, Gasmengendurchsatz oder pV-Durchsatz.
Stellen Sie sich vor, Sie möchten für Ihren Umzug einen LKW mieten. Der Vermieter gibt Ihnen als Kenngröße eine Ladekapazität in m3 an. Diese Information ist für Sie nur bedingt hilfreich, da Sie gleichzeitig die »mittlere Dichte« Ihres Ladeguts wissen müssen, um das Fahrzeug nicht zu überladen. Ebenso verhält es sich mit den Begriffen Saugvermögen und Saugleistung. Bei zu hohen Drücken (zu hoher Gasdichte) nimmt das Saugvermögen von Hochvakuumpumpen dramatisch ab, so dass sie nur in vorgegebenen Druckbereichen optimal arbeiten.
Das Saugvermögen ist also seinerseits druckabhängig, und wir können für die transportierte Gasmenge oder den pV- Durchfluss qpV schreiben:
qpV = p · S(p) (7)
Die Zahlen für das Saugvermögen, die man auf den Typenschildern von Hochvakuumpumpen liest, sind sehr beeindruckend und für den Laien oft irritierend. So gibt es z.B. Öldiffusionspumpen mit S = 50.000 l/s oder Turbomolekularpumpen mit S = 5.000 l/s. (Man stelle sich eine Flüssigkeitspumpe vor, die die unglaubliche Menge von 50 m3 pro Sekunde transportieren kann!). Entscheidend dabei ist, dass diese Zahlen erst für Drücke unterhalb von 10-3 mbar gelten, für wesentlich höhere Drücke geht S dramatisch nach unten (Übergang von molekularer zu viskoser Strömung). Die bei 10-3 mbar tatsächlich vorhandene Saugleistung liegt dann für die beiden genannten Beispiele bei 50 bzw. 5 mbar . l/s.
Im nächsten Newsletter werden wir uns mit Leitwerten und verschiedenen Typen von Vakuumpumpen beschäftigen.
Letzte Änderung: